一、语句覆盖
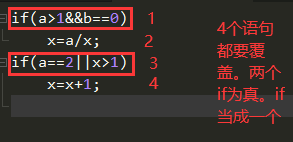
case1:a=2、b=0、x=3
二、判定覆盖
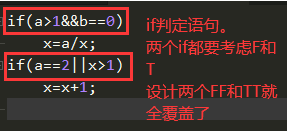
case1:a=1、b=0、x=1
case2:a=2、b=0、x=3
三、条件覆盖
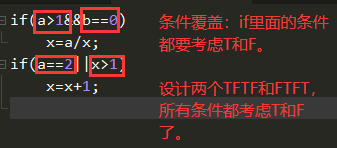
case1:a=1、b=0、x=3
case2:a=2、b=1、x=1
四、条件判定覆盖

case1:a=2、b=0、x=3
case2:a=2、b=1、x=1
case3:a=1、b=0、x=3
case4:a=1、b=1、x=1
五、路径覆盖
语句覆盖、判定覆盖、条件覆盖、判定条件覆盖这四种覆盖方法都在一定程度上进行测试路径的覆盖,但每种方法都无法做到100%覆盖,都存在漏测的方法。
路径覆盖期望将被测对象的所有路径都能验证到,对于比较简单的代码而言,实现100%路径覆盖是可能的,但如果代码中出现较多判定和较多循环时,路径数目将急剧增长,要在测试中覆盖所有路径几乎不可能或投入成本可能很高。有必要把覆盖路径数量压缩到一定的限度内。
基本路径测试方法包括以下4个步骤:
- 画出程序的控制流图。
- 计算程序的环形复杂度,导出程序基本路径集中的独立路径条数,这是确定程序中每个可执行语句至少执行一次所必须的测试用例数目的上界。
- 导出基本路径集,确定程序的独立路径。
- 根据3中的独立路径,设计测试用例的输入数据和预期输出。
案例:闰年算法路径覆盖率计算
Int IsLeap(int year){
if(year%4==0){
if(year%100==0){
if(year%400==0)
leap=1;
else
leap=0;
}else
leap=1;
}else
leap=0;
return leap;
}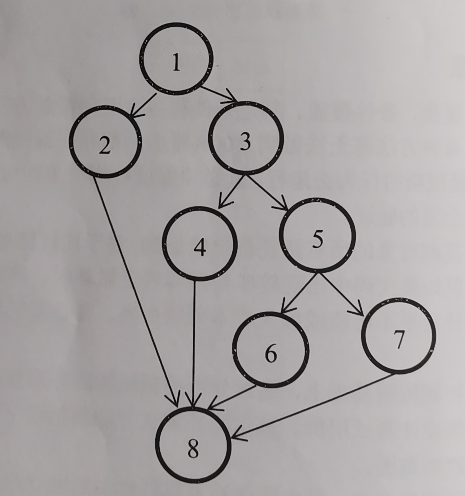
每个圈代表代码中的逻辑语句,如下:
1.if(year%4==0)
2.leap=0;
3.if(year%100==0)
4.leap=1;
5.if(year%400==0)
6.leap=1;
7.leap=0;
8.return leap;
计算圈复杂度
根据公式∶V(G)=E-V+2P
其中E表示程序控制流程图中边的数量,V表示流程图中节点的数量,P则表示流程图中连接组件的数量。图7-21所有组件是相通的,没有独立的部分,因此P为1。
综合上述,E=10,共计有10条边,即连接线,V=8,共计有8个节点,即8个圆圈,则圈复杂度为∶
V(G)=10-8+2*1=4
归结基础路径
可归结为四条基本路径∶
P1:1、2、8
P2:1、3、4、8
P3:1、3、5、6、8
P4:1、3、5、7、8
设计测试用例:
根据以上4条基本路径设计测试用例如下∶
Casel∶不能被4整除∶1999
Case2∶能被4整除,能被100整除,能被400整除∶2000
Case3∶能被4整除,能被100整除,不能被400整除∶1900
Case4∶能被4整除,不能被100整除∶2004