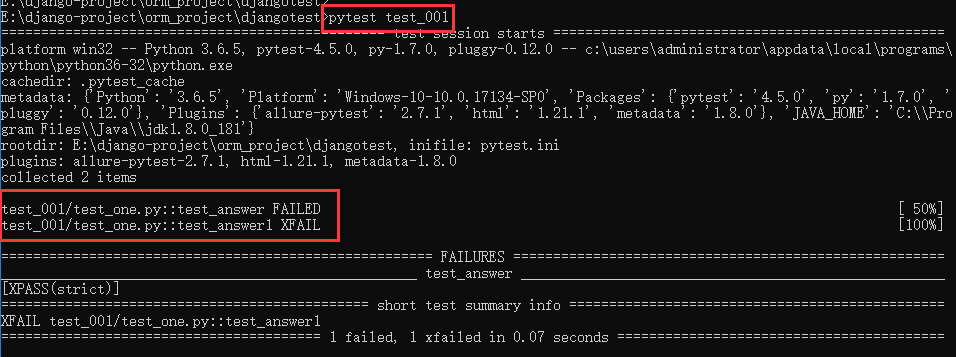
正交法
本质上是用数学中的数据统计【统计学】中的方法进行测试。
通过正交法可以用少量测试用例来覆盖大多数的测试情况
概念
因子【k】:表示的是输入的条件,每列是一个因子
水平【 m 】:表示的是输入的条件所得到的结果,表格中的每个小格是一个结果
测试思想
1)使用每个控件的每个取值参与组合的次数是基本相等的(均匀的)
2)在所有的组合数据中,选取数据时,应该均匀的选取,而不能从局部选取。
3)如果时间允许,尽可能的多测一些组合
正交表:主要针对一个输入框里面可能有多个值,而且数量巨大
设计步骤
第一步:需求分析,确定因素和水平【其实就是找有几个输入和几个结果】
第二步:根据因子和水平的数量,确定选择哪个正交表。
第三步:将具体的值替换掉正交表中的内容
第四步:根据经验补充实验次数(一般是全选相同水平。)
第五步:根据正交表写测试用例
应用场景
在一个界面中有多个控件,每个控件有多个取值,测试时考虑不同的控件不同取值之间的多种组合,但组合数量巨大(>20种,20种以下一般考虑判定表因果图),没有必要全部测试,如何从所有的组合中挑选最少、最优的组合进行测试,可以使用正交排列法。
年龄 体重 省 市 县 。比如:输入年龄 18,体重45,山西 大同 阳高
比如多选择组合,这种情况:
案例
因子数及水平数与正交实验表相符,直接使用,不作介绍
案例一:因子数与正交实验表因子数不相符
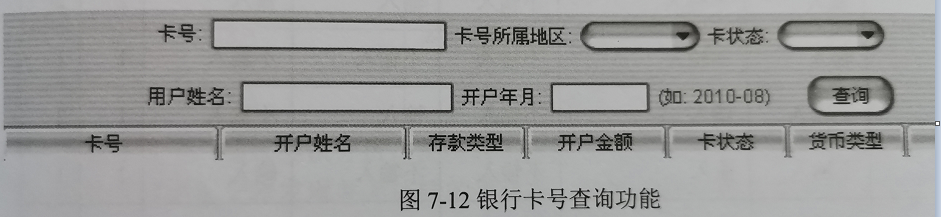
步骤一:确定因子、水平。
因子:卡号、所属地、卡状态、用户姓名、开户年月5个查询条件,为5因子;
水平:假设每个查询条件仅设定输入和不输入,则为2水平。
步骤二:根据因子、水平。选择合适的正交实验表
5因子2水平,在正交表中仅有3因子2水平,7因子2水平,11因子2水平等因子数更高的正交表。
在水平数相同时,选择因子数稍大于输入参数个数,且实验次数最少的正交表。
因此这里选择:7因子2水平的正交表。
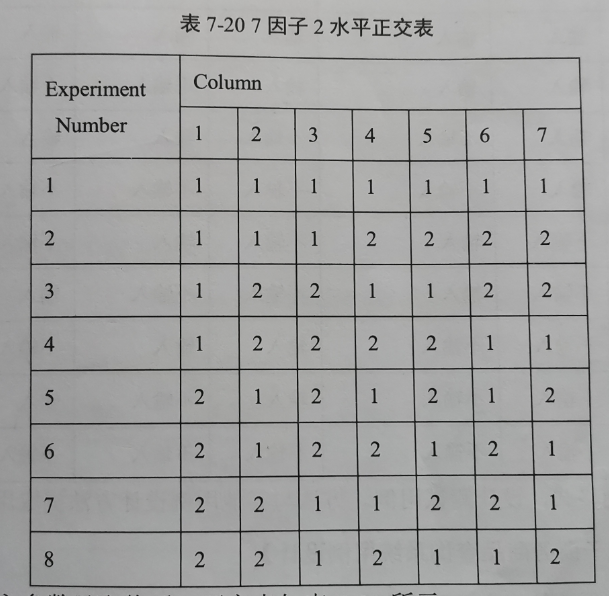
步骤三:替换相应参数及取值
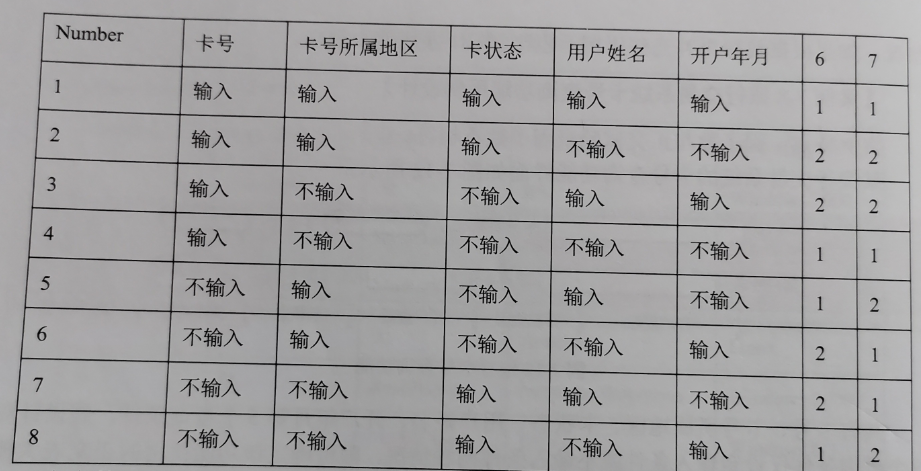
步骤四:根据经验补充用例
补充所有因子全部取相同水平的情况。这里取5个因子全部选择水平2的情况。即全部取不输入的情况

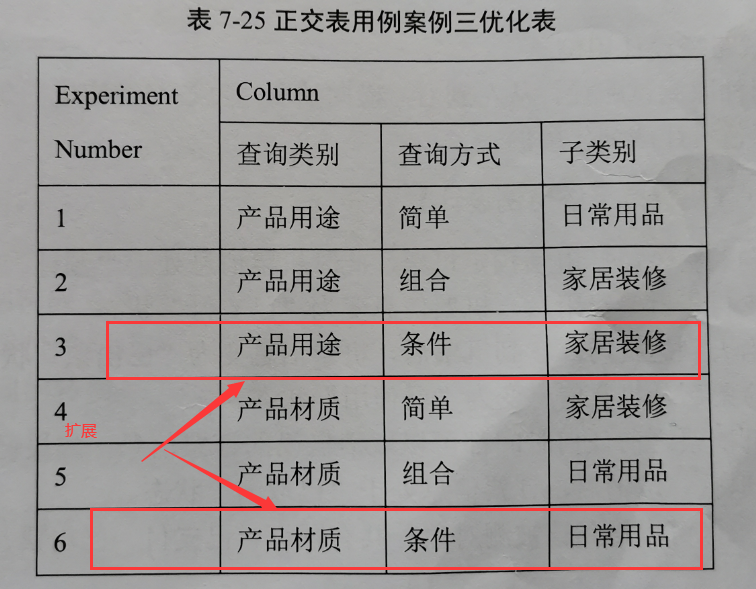
案例二:水平数与正交实验表不相符
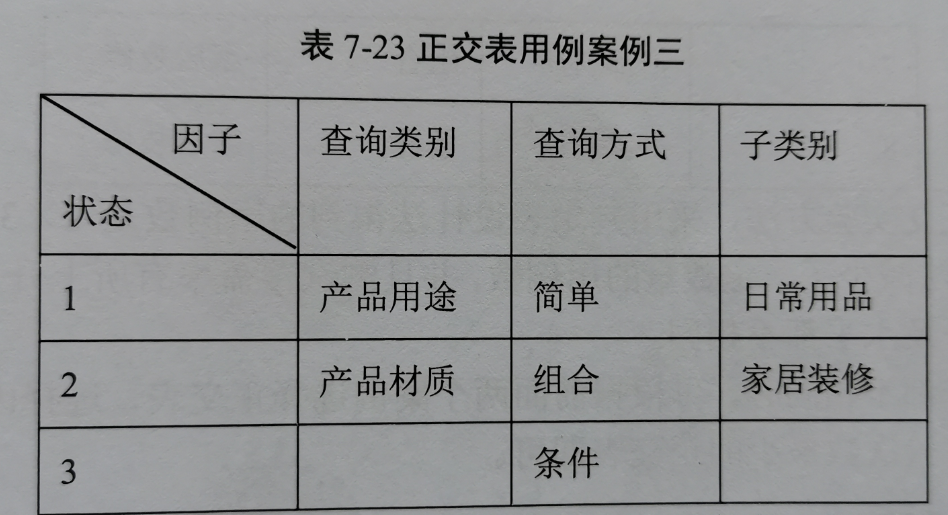
这里是3个因子。但是水平有可能是2也可能是3。预期最接近的正交表是3因子2水平及4因子3水平。
而4因子3水平的实验次数是9,3因子2水平的实验次数是4。并且因子数与需求是一样。所以这里我们通过先合并水平再扩展水平的方法选择正交表。
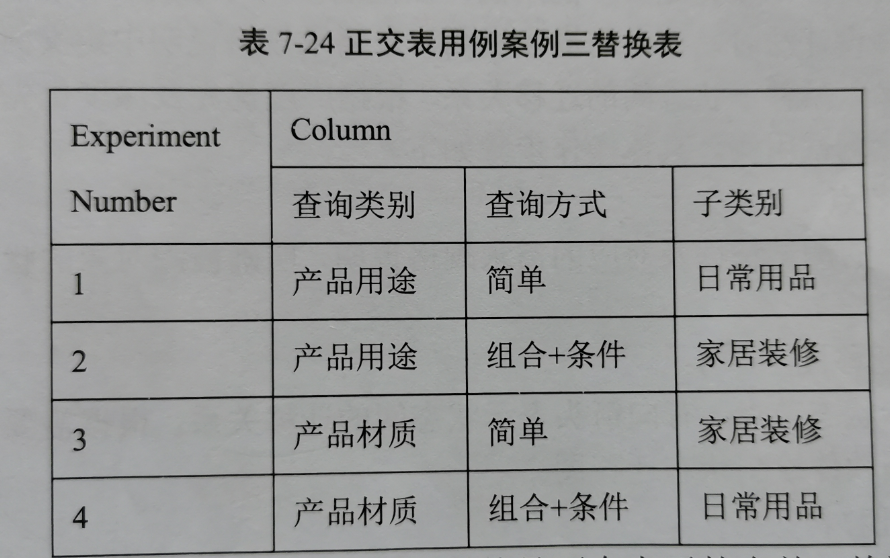
填充完后,再进行扩展。并根据经验得到下面的表